過去問H19年 第10問
次の製品別の販売価格および原価等のデータに基づき、下記の設問に答えよ。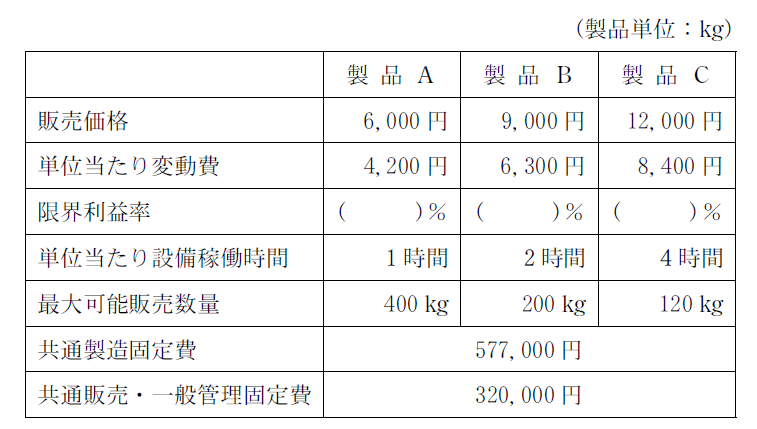 
（設問1） 損益分岐点売上高として最も適切なものはどれか（単位：円）。 ア 2,900,000 イ 2,909,000 ウ 2,990,000 エ 2,999,000
（設問2） 最大可能な設備稼働時間が1,000時間であるとき、営業利益を最大にする 各製品の実現可能な販売数量の組み合わせとして最も適切なものはどれか （単位：kg）。 ア Ａ：120 Ｂ：200 Ｃ：120 イ Ａ：200 Ｂ：200 Ｃ：100 ウ Ａ：400 Ｂ： 60 Ｃ：120 エ Ａ：400 Ｂ：200 Ｃ： 50
(設問1)解説
答え ウ
設問1は損益分岐点売上高を求める問題ですね。 損益分岐点は固定費総額と限界利益が同じになる売上高を計算します。
制約条件が最大販売数量しか設定されていないので限界利益率が大きいものから販売していけばいいですね。 表の限界利益率が空欄になっているので計算します。
上記の計算式を使ってそれぞれの限界利益率を計算すると、
となります。 限界利益率はすべて同じになりました。 この場合はどのように販売しても損益分岐点は同じになります。 損益分岐点売上高は、
で計算することができますが、今回の問題では最大可能販売数量が決まっているので万が一すべて売っても黒字にならない可能性があるので、今回は製品Aから順番に販売していくことにしましょう。
固定費総額が897,000円なのでまだ損益分岐点に届きませんね。 なので、今度は製品Bを販売していきます。
製品Bもすべて販売したとすると、損益分岐点を超えてしまいますね。 720,000 + 540,000 ＞ 固定費総額 879,000 製品A、Bをすべて販売すれば固定費を回収できるというのがわかったので、固定費総額を限界利益率で割って損益分岐点売上高を求めればいいですね。
ということで答えは ウ 2,990,000 です。
(設問2)解説
答え エ
設問2では新たに設備稼働時間が1,000時間という制約ができました。 限界利益率はどの製品も同じなので、この場合は1時間当たりの限界利益が高いものから生産していくのがベストですね！
各製品の限界利益と設備稼働時間を見ると、
となります。 1時間当たりの限界利益は限界利益を稼働時間で割ってあげればいいですね。
ということで、製品A→B→Cの順に生産していけばいいですね。
答えは エ Ａ：400 Ｂ：200 Ｃ： 50 ですね。
やっぱりこういう計算問題はたくさん解いて慣れるしかないですね。 何度も言っていますが、公式を丸暗記するのではなく、どうしてこの公式になるのかを理解すると覚えやすいし、応用が利きます。 諦めず、時間をかけて解いていきましょう！